SOAL PENYELESAIANNYA MENGGUNAKAN MATRIKS
SOAL PENYELESAIANNYA MENGGUNAKAN MATRIKS
NAMA : RYAN ALFARIDZI
KELAS : XI IPS 2
ABSEN : 31
Determinan Matriks Ordo 2 x 2
Contoh matriks dengan ordo 2 x 2 adalah seperti ini:
Penyelesaian:
kita bisa menggunakan rumus untuk bisa menyelesaikannya.
Det (A) = |A| = ad – bc
|A| = (7 x 3) – (2 x 8)
|A| = 21 – 16
|A| = 5
Determinan Matriks Ordo 3 x 3
Contoh matriks dengan ordo 3 x 3 adalah seperti ini:
Untuk menghitung determinan matriks berordo 3×3, kamu bisa menggunakan aturan Sarrus. Gambar di bawah ini akan menunjukkan caranya dengan lebih jelas.

Sumber Gambar: idschool.net
Contoh Soal :
1. Hitunglah berapa nilai determinan dari matriks ordo 3 x 3 berikut ini :

pembahasan:

det( A ) = ( 1 . 1 . 2 ) + ( 2 . 4 . 3 ) + ( 3 . 2 . 1 ) – ( 3 . 1 . 3 ) – ( 1 . 4 . 1 ) – ( 2 . 2 . 2 )
= 2 + 24 + 6 – 9 – 4 – 8
= 11
Kofaktor Matriks ber-ordo 2 x 2 dan 3 x 3
Contoh:
1. Tentukan kofaktor dari minor matriks berikut ini :
pembahasan:
KEab = (-1)a+b x NEab
KE11 = (-1)1+1 x NE11 = (-1)2 x (-3) = 1 x -3 = -3
KE12 = (-1)1+2 x NE12 = (-1)3 x (-6) = -1 x (-6) = 6
KE13 = (-1)1+3 x NE12 = (-1)4 x (-3) = 1 x (-3) = -3
KE21 = (-1)2+1 x NE21 = (-1)3 x (-6) = -1 x (-6) = 6
KE22 = (-1)2+2 x NE22 = (-1)4 x (-12) = 1 x (-12) = -12
KE23 = (-1)2+3 x NE23 = (-1)5 x (-6) = -1 x (-6) = 6
KE31 = (-1)3+1 x NE31 = (-1)4 x (-3) = 1 x (-3) = -3
KE32 = (-1)3+2 x NE32 = (-1)5 x (-6) = -1 x (-6) = 6
KE33 = (-1)3+3 x NE33 = (-1)6 x (-3) = 1 x (-3) = -3
Maka kofaktornya adalah :
Invers Matriks ber-ordo 2 x 2
Contoh Soal :
1. Tentukanlah invers dari matriks berikut.

Pembahasan:

Catatan: elemen-elemen yang berada di lingkar biru merupakan diagonal utama matriks A yang ditukar posisinya, sedangkan elemen-elemen yang berada di lingkar oranye merupakan diagonal kedua matriks A yang dikalikan dengan minus satu (-1).
Invers Matriks ber-ordo 3 x 3
Contoh Soal :
1. Tentukan invers matriks berikut dengan menggunakan adjoin!

Penyelesaian:

Oke, berdasarkan rumus di atas, kita membutuhkan determinan dan adjoin matriks A. Pertama, kita cari terlebih dahulu determinan matriks A menggunakan metode yang sudah dijelaskan sebelumnya. Bisa dengan cara aturan Sarrus ataupun metode minor-kofaktor. Misalnya, kita akan menggunakan metode Sarrus, sehingga:

Kemudian, kita tentukan adjoin matriks dengan mencari kofaktor matriks A tersebut.

Oleh karena itu,

Jadi,




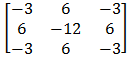
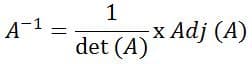
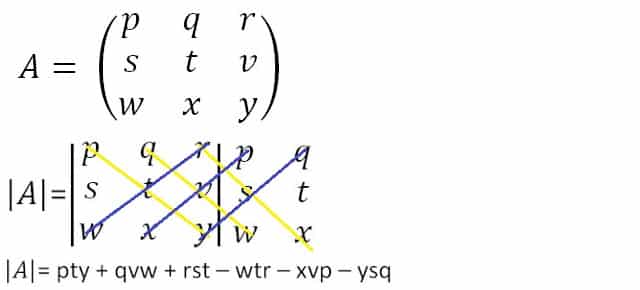


Tidak ada komentar:
Posting Komentar