SOAL DAN PEMBAHASAN TRIGONOMETRI: LIMIT DAN KONSEP LIMIT FUNGSI ALJABA

Assalamualaikum Wr.Wb
Ryan Alfaridzi (32) XI IPS 2

Pengertian Limit Fungsi

Limit merupakan sebuah konsep matematika dimana sesuatu dikatakan “hampir” atau “mendekati” nilai suatu bilangan tertentu. Limit dapat berupa sebuah fungsi yang kodomainnya “hampir” atau “mendekati” nilai suatu bilangan asli tertentu.

Sifat-sifat Limit Fungsi Aljabar

Apabila n merupakan bilangan bulat positif, k konstanta, f dan g adalah fungsi yang mempunyai limit di c, maka sifat-sifat di bawah ini berlaku.
Ada tiga metode dalam mengerjakan limit fungsi aljabar, yaitu:

1. Metode substitusi

Metode paling mudah dengan menentukan hasil suatu limit fungsi adalah dengan mensubstitusi langsung nilai kedalam fungsi f(x). Syarat metode ini adalah jika hasil substitusi tidak membentuk nilai “tak tentu”. Contoh:
$\lim \limits_{x\to 3}\frac{x^2 - 4}{x + 2} = \frac{9 - 4}{3 + 2} = 1$

2. Metode pemfaktoran
Jika pada metode substitusi menghasilkan suatu nilai bentuk tak tentu seperti:
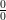∞, $\frac{0}{0}$ , $\frac{\infty}{\infty}$ , 0 x∞, ∞ – ∞, 00, ∞0, atau ∞∞
maka fungsi tersebut harus difaktorkan terlebih dahulu sehingga bentuknya tidak menjadi bentuk tak tentu, baru kemudian bisa disubstitusikan $x\to c$ . Contoh:

$\lim \limits_{x\to 3}\frac{x^2 - 3x}{2x - 6} = \frac{x(x - 3)}{2(x - 3)} = \frac{3}{2}$

3. Metode perkalian dengan akar sekawan
Metode ini digunakan jika pada metode substitusi langsung menghasilkan nilai limit yang irasional. Fungsi dikalikan dengan akar sekawannya agar bentuk limit tersebut tidak irasional, sehingga bisa dilakukan kembali substitusi langsung nilai $x\to c$ . Contoh:

$\lim \limits_{x\to -1}\frac{x +1}{1 - \sqrt{x + 2}} x (\frac{1 + \sqrt{x +2}}{1 + \sqrt{x + 2}}) = \frac{(x + 1)(1 + \sqrt{x+ 2})}{1 - (x + 2)}$
$=\frac{(x + 1)(1+\sqrt{x+2})}{-x - 1} = \frac{(x+1)(1+\sqrt{x+2})}{-(x+1)} = -(1 + \sqrt{x + 2})$
$=-(1 + \sqrt{-(1) + 2}) = -(1 + 1) = -2$
Ada dua metode dalam mengerjakan limit fungsi aljabar bentuk tak berhingga:
Membagi dengan pangkat tertinggi
Metode ini digunakan pada limit fungsi bentuk $\lim \limits_{x\to \infty}\frac{f(x)}{g(x)}$ . Metode ini dapat dikerjakan dengan membagi pembilang f(x) dan penyebut g(x) dengan variabel xn berpangkat tertinggi yang ada dalam fungsi f(x) dan g(x). Setelahnya, baru dapat disubstitusi dengan $x\to \infty$ . Contoh:
$\lim \limits_{x\to \infty}\frac{4x-1}{x^2+2} = \frac{\frac{4x}{x^2} - \frac{1}{x^2}}{\frac{x^2}{x^2} + \frac{2}{x^2}} = \frac{\frac{4}{x} - \frac{1}{x^2}}{1+\frac{2}{x^2}} = \frac{0}{1} = 0$
Mengalikan bentuk sekawan
Metode ini digunakan pada limit fungsi bentuk 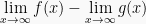$\lim \limits_{x\to \infty}f(x) - \lim \limits_{x\to \infty}g(x)$ . Metode ini dapat diselesaikan dengan perkalian bentuk sekawan:
$\frac{\lim \limits_{x\to \infty}f(x)+\lim \limits_{x\to \infty}g(x)}{\lim \limits_{x\to \infty}f(x)+\lim \limits_{x \to \infty}g(x)}$
kemudian dilanjutkan pembagian dengan metode pertama yaitu membagi dengan pangkat tertinggi. Contoh:
$\lim \limits_{x\to \infty}(\sqrt{x^2 + 4x - 5 - \sqrt{x^2 -x -2}})$
$=\lim \limits_{n\to \infty}(\sqrt{x^2 + 4x -5 - \sqrt{x^2 - x - 2}})$ $x \frac{(\sqrt{x^2+4x-5 + \sqrt{x^2 - x - 2}})}{(\sqrt{x^2+4x-5} + \sqrt{x^2-x-2})}$
$= \lim \limits_{n\to \infty}\frac{((x^2+4x-5) - (x^2-x-2))}{(\sqrt{x^2+4x-5} + \sqrt{x^2-x-2})}$ $= \lim \limits_{n\to \infty}frac{5x-3}{(\sqrt{x^2+4x-5})+\sqrt{x^2-x-2}}$
Kemudian pembilang dan penyebut dibagi x pangkat tertinggi yaitu x1:
$\lim \limits_{n\to \infty}\frac{\frac{5x}{x}-\frac{3}{x}}{(\sqrt{\frac{x^2+4x-5}{x^2}}+\sqrt{\frac{x^2-x-2}{x^2}})}$ $= \lim \limits_{n\to \infty}\frac{5-\frac{3}{x}}{(\sqrt{1+\frac{4}{x}-\frac{5}{x^2}}+ \sqrt{1-\frac{1}{x}-\frac{2}{x^2}})}$
$= \frac{(-0}{(1+1)} = \frac{5}{2}$

Contoh Soal Limit Fungsi dan Pembahasan

Contoh Soal Limit 1

Tentukanlah nilai dari $\lim_{x\to 2}(\frac{6-x}{x^2-4} - \frac{1}{x-2})$ (UAN 2002)
Pembahasan 1 :
$\lim \limits_{x\to 2}(\frac{6-x}{x^2} - \frac{1}{x-2}) = \lim \limits_{x\to 2}(\frac{6-x}{x^2-4} - \frac{x+2}{(x-2)(x+2)})$ $= \lim \limits_{x\to 2}\frac{(6-x) - (x+2)}{(x-2)(x+2)}$
$=\lim \limits_{x\to 2}\frac{4-2x}{(x-2)(x+2)} = \lim \limits_{x\to 2}\frac{-2(x-2)}{(x-2)(x+2)}$ $= \lim \limits_{x\to 2}\frac{-2}{(x+2)}$
$=-\frac{2}{4} = -\frac{1}{2}$

Konsep Limit Fungsi

Konsep limit fungsi ini adalah hal yang utama harus ditahui sebelum masuk ke materi lanjutan. konsep limit fungsi ini sangat diperlukan dalam mempelajari limit lebih jauh. Penentuan limit suatufungsi di suatu titik c, sangat bergantung pada kedudukan titik c dan domain fungsi tersebut.Dalam pembahasan limit fungsi, yang menjadi domain fungsi adalah himpunan bilangan real dimana fungsi tersebut terdefnisi. Sebuah fungsi f dikatakan mempunyai limit di titik c jika dan hanya jika nilai fungsi untuk x dari kiri dan kanan menuju ke bilangan yang sama. Suatu fungsi f mempunyai nilai limit di titik c, apabila nilai limit kiri sama dengan nilai limit kanan dari fungsi tersebut pada titik c. Tidak semua fungsi mempunyai limit di titik c. Titik c tidak harus anggota domain fungsi, tetapi c anggota himpunan bilangan real.

Untuk lebih memahami limit fungsi, anda dapat melihat contoh soal dan pembahasan limit fungsi pada subbab D.

Sifat-sifat Limit Fungsi Aljabar

Misalkan f sebuah fungsi f : R → R dan misalkan L, dan c anggota himpunan bilangan real.
Misalkan f(x), g(x) adalah fungsi yang mempunyai nilai limit pada x mendekati c, dengan k dan c adalah bilangan real serta n adalah bilangan positif, maka

Menentukan Nilai Limit Fungsi Aljabar

Dalam menentukan nilai limit fungsi Aljabar, ada beberapa langkah yang harus dilakukan. Berikut adalah Langkah-langkah menentukan nilai limit fungsi aljabar.

Substitusikan x = c ke fungsi f(x) sehingga diperoleh f(c) = L. (L = nilai tentu).
Jika L merupakan salah satu bentuk tak tentu maka kita harus mencari bentuk tentu limit fungsi tersebut dengan memilih strategi: mencari beberapa titik pendekatan, dan memfaktorkan.
(Manullang dkk., 2017)

SOAL DAN PEMBAHASAN TRIGONOMETRI

Senin, 11 Januari 2021

LIMIT DAN KONSEP LIMIT FUNGSI ALJABA

Limit merupakan sebuah konsep matematika dimana sesuatu dikatakan “hampir” atau “mendekati” nilai suatu bilangan tertentu. Limit dapat berupa sebuah fungsi yang kodomainnya “hampir” atau “mendekati” nilai suatu bilangan asli tertentu.

Apabila n merupakan bilangan bulat positif, k konstanta, f dan g adalah fungsi yang mempunyai limit di c, maka sifat-sifat di bawah ini berlaku.
Ada tiga metode dalam mengerjakan limit fungsi aljabar, yaitu:

Metode paling mudah dengan menentukan hasil suatu limit fungsi adalah dengan mensubstitusi langsung nilai kedalam fungsi f(x). Syarat metode ini adalah jika hasil substitusi tidak membentuk nilai “tak tentu”. Contoh:
$\lim \limits_{x\to 3}\frac{x^2 - 4}{x + 2} = \frac{9 - 4}{3 + 2} = 1$

$\lim \limits_{x\to 3}\frac{x^2 - 3x}{2x - 6} = \frac{x(x - 3)}{2(x - 3)} = \frac{3}{2}$

Untuk lebih memahami limit fungsi, anda dapat melihat contoh soal dan pembahasan limit fungsi pada subbab D.

Sifat-sifat Limit Fungsi Aljabar

Misalkan f sebuah fungsi f : R → R dan misalkan L, dan c anggota himpunan bilangan real.
Misalkan f(x), g(x) adalah fungsi yang mempunyai nilai limit pada x mendekati c, dengan k dan c adalah bilangan real serta n adalah bilangan positif, maka

Menentukan Nilai Limit Fungsi Aljabar

Substitusikan x = c ke fungsi f(x) sehingga diperoleh f(c) = L. (L = nilai tentu).
Jika L merupakan salah satu bentuk tak tentu maka kita harus mencari bentuk tentu limit fungsi tersebut dengan memilih strategi: mencari beberapa titik pendekatan, dan memfaktorkan.
(Manullang dkk., 2017)

Contoh Soal Limit Fungsi Aljabar

Untuk lebih memahami limit fungsi, perhatikanlah contoh soal dan pembahasan limit fungsi berikut ini.

DAFTAR PUSTAKA

https://rumusrumus.com/limit-fungsi-aljabar/
https://tambahpinter.com/limit-fungsi/

Tidak ada komentar:

Posting Komentar

SIFAT-SIFAT LIMIT DAN CONTOH SOALNYA SERTA SOAL KONTEKSTUAL YANG BERHUBUNGAN DENGAN LIMIT

Total Tayangan Halaman

Senin, 11 Januari 2021

LIMIT DAN KONSEP LIMIT FUNGSI ALJABA

Limit merupakan sebuah konsep matematika dimana sesuatu dikatakan “hampir” atau “mendekati” nilai suatu bilangan tertentu. Limit dapat berupa sebuah fungsi yang kodomainnya “hampir” atau “mendekati” nilai suatu bilangan asli tertentu.

Apabila n merupakan bilangan bulat positif, k konstanta, f dan g adalah fungsi yang mempunyai limit di c, maka sifat-sifat di bawah ini berlaku.Ada tiga metode dalam mengerjakan limit fungsi aljabar, yaitu:

Metode paling mudah dengan menentukan hasil suatu limit fungsi adalah dengan mensubstitusi langsung nilai kedalam fungsi f(x). Syarat metode ini adalah jika hasil substitusi tidak membentuk nilai “tak tentu”. Contoh:

Tentukanlah nilai dari (UAN 2002)Pembahasan 1 :

Untuk lebih memahami limit fungsi, anda dapat melihat contoh soal dan pembahasan limit fungsi pada subbab D.

Sifat-sifat Limit Fungsi Aljabar

Misalkan f sebuah fungsi f : R → R dan misalkan L, dan c anggota himpunan bilangan real.Misalkan f(x), g(x) adalah fungsi yang mempunyai nilai limit pada x mendekati c, dengan k dan c adalah bilangan real serta n adalah bilangan positif, maka

Menentukan Nilai Limit Fungsi Aljabar

Substitusikan x = c ke fungsi f(x) sehingga diperoleh f(c) = L. (L = nilai tentu).Jika L merupakan salah satu bentuk tak tentu maka kita harus mencari bentuk tentu limit fungsi tersebut dengan memilih strategi: mencari beberapa titik pendekatan, dan memfaktorkan.(Manullang dkk., 2017)

Contoh Soal Limit Fungsi Aljabar

Untuk lebih memahami limit fungsi, perhatikanlah contoh soal dan pembahasan limit fungsi berikut ini.DAFTAR PUSTAKA

https://rumusrumus.com/limit-fungsi-aljabar/https://tambahpinter.com/limit-fungsi/

Tidak ada komentar:

Posting Komentar

SIFAT-SIFAT LIMIT DAN CONTOH SOALNYA SERTA SOAL KONTEKSTUAL YANG BERHUBUNGAN DENGAN LIMIT

Apabila n merupakan bilangan bulat positif, k konstanta, f dan g adalah fungsi yang mempunyai limit di c, maka sifat-sifat di bawah ini berlaku.
Ada tiga metode dalam mengerjakan limit fungsi aljabar, yaitu:

Metode paling mudah dengan menentukan hasil suatu limit fungsi adalah dengan mensubstitusi langsung nilai kedalam fungsi f(x). Syarat metode ini adalah jika hasil substitusi tidak membentuk nilai “tak tentu”. Contoh:
$\lim \limits_{x\to 3}\frac{x^2 - 4}{x + 2} = \frac{9 - 4}{3 + 2} = 1$

Misalkan f sebuah fungsi f : R → R dan misalkan L, dan c anggota himpunan bilangan real.
Misalkan f(x), g(x) adalah fungsi yang mempunyai nilai limit pada x mendekati c, dengan k dan c adalah bilangan real serta n adalah bilangan positif, maka

Substitusikan x = c ke fungsi f(x) sehingga diperoleh f(c) = L. (L = nilai tentu).
Jika L merupakan salah satu bentuk tak tentu maka kita harus mencari bentuk tentu limit fungsi tersebut dengan memilih strategi: mencari beberapa titik pendekatan, dan memfaktorkan.
(Manullang dkk., 2017)

Untuk lebih memahami limit fungsi, perhatikanlah contoh soal dan pembahasan limit fungsi berikut ini.

DAFTAR PUSTAKA

https://rumusrumus.com/limit-fungsi-aljabar/
https://tambahpinter.com/limit-fungsi/