SOAL DAN PEMBAHASAN TRIGONOMETRI: TRANSFORMASI TRANSLASI, REFLEKSI, ROTASI, DILATASI, DENGAN MATRIKS

TRANSFORMASI TRANSLASI, REFLEKSI, ROTASI, DILATASI, DENGAN MATRIKS

RYAN ALFARIDZI (31) XI IPS 2

Translasi

Translasi atau pergeseran adalah suatu transformasi yang memindahkan tiap titik pada bidang dengan jarak dan arah tertentuk.

1. Bayangan garis y = 2x + 2 yang dicerminkan terhadap garis y= x adalah. . .

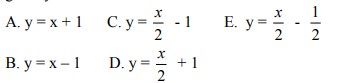
soal transformasi geometri no 1

Jawaban : C

Pembahasan :

soal transformasi geometri dan jawaban no 1

2. Persamaan bayangan kurva y = x² – 2x – 3 oleh rotasi [0, 180°], kemudian dilanjutkan oleh pencerminan terhadap garis y = -x adalah ….

A. y = x² – 2x – 3

B. y = x² – 2x + 3

C. y = x² + 2x + 3

D. x = y² – 2y – 3

E. x = y² + 2y + 3

Jawaban : D

Pembahasan :

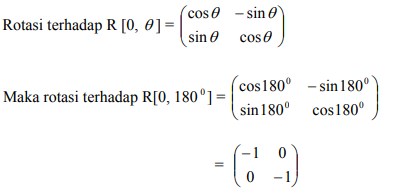
soal transformasi geometri dan jawaban no 2

Rotasi sudut-sudut yang lain dapat dihitung sendiri menggunakan kaidah trigonometri.

pencerminan terhadap garis y = -x

soal transformasi geometri dan jawaban no 2-1

3. Hasil translasi titik P1(3, –2) oleh T1 dilanjutkan dengan T2,

$T_{2} = \begin{pmatrix} 2 \\ 1 \end{pmatrix}$

menghasilkan titik P2 (8, 7). Komponen translasi dari T1 yang sesuai adalah ….

$\textrm{A.} \; \; \; \begin{pmatrix} 8 \\ 3 \end{pmatrix}$

$\textrm{B.} \; \; \; \begin{pmatrix} 3 \\ 8 \end{pmatrix}$

$\textrm{C.} \; \; \; \begin{pmatrix} 3 \\ 5 \end{pmatrix}$

$\textrm{D.} \; \; \; \begin{pmatrix} 1 \\ 8 \end{pmatrix}$

$\textrm{E.} \; \; \; \begin{pmatrix} 1 \\ 5 \end{pmatrix}$

Pembahasan:

Misalkan:

$T_{1} = \begin{pmatrix} a \\ b \end{pmatrix}$

Maka,

$T_{2} \bullet T_{1} = \begin{pmatrix} a + 4 \\ b + 1 \end{pmatrix}$

Perhatikan proses translasi berikut.

Mencari nilai a:

3 + a + 2 = 8
a + 5 = 8
a = 8 – 5 = 3

Mencari nilai b:

-2 + b + 1 = 7
b – 1 = 7
b = 7 + 1 = 8

Jadi, nilai translasi dari T1 adalah

$T_{1} = \begin{pmatrix} 3 \\ 8 \end{pmatrix}$

Jawaban: B

4. Persamaan garis 3x – y – 11 = 0 karena refleksi terhadap garis y = x, dilanjutkan oleh transformasi yang bersesuaian dengan matriks A,

$\begin{pmatrix} -3 & 2 \\ -1 & 1 \end{pmatrix}$

adalah ….
A. –2x – 7y –11 = 0
B. 2x + 7y – 11 = 0
C. –2x – 7y + 11 = 0
D. 2y – 7x + 11 = 0
E. 2x – 7y + 11 = 0

Pembahasan:

Pertama, cari hasil bayangan dari pencerminan terhadap garis y = x.

Matriks pencerminan terhadap garis y = x adalah:

Berdasarkan rumus di atas, dapat diperoleh kesimpulan bahwa x’ = y dan y’ = x. Substitusikan nilai tersebut pada persamaan 3x – y – 11 = 0 sehingga diperoleh persamaan berikut.

3x – y – 11 = 0
3y’ – x’ – 11 = 0
– x’ + 3y’ – 11 = 0

Kedua, langkah selanjutnya adalah transformasi yang bersesuaian dengan matriks A,

$\begin{pmatrix} -3 & 2 \\ -1 & 1 \end{pmatrix}$

Perhatikan langkah – langkahnya seperti berikut,

$\begin{pmatrix} x'' \\ y'' \end{pmatrix} = \begin{pmatrix} -3 & 2 \\ -1 & 1 \end{pmatrix} \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} -3x' + 2y' \\ -x' + y' \end{pmatrix}$

Sehingga, diperoleh dua persamaan berikut.

–3x’ + 2y’ = x’’
– x’ + y’ = y’’

Berikutnya, akan dicari persamaan yang senilai dengan x’ dan y’:

Mencari nilai x’:

Metode eliminasi variabel

Mencari nilai y’:

Metode eliminasi variabel

Subtitusi hasil x’ dan y’ di atas pada persamaan – x’ + 3y’– 11 = 0:

$-x' + 3y' - 11 = 0$

$-\left( 2y'' - x'' \right) + 3\left( 3y'' - x'' \right) - 11 = 0$

$-2y'' + x'' + 9y'' - 3x'' - 11 = 0$

$-2x'' + 7y'' - 11 = 0$

$2x'' - 7y'' + 11 = 0$

Jadi, hasil akhir transformasi dari persamaan 3x – y – 11 = 0 adalah 2x – 7y + 11 = 0.

Jawaban: E

5. Hasil pencerminan garis x – 2y – 2 = 0 terhadap sumbu y dan kemudian diputar dengan R[ O(0,0), 90o ] adalah ….

A. 2x – y – 4 = 0
B. x – 2y – 4 = 0
C. x – 2y – 2 = 0
D. 2x – y + 2 = 0
E. 2x – y – 4 = 0 \]

Pembahasan:

Hasil transformasi pencerminan terhadap sumbu y adalah:

Contoh Soal dan Pembahasan Transformasi Geometri Refleksi

Sehingga diperoleh x’ = – x dan y’ = y, selanjutnya substitusikan kedua nilai yang diperoleh pada persamaan x – 2y – 2 = 0.

x – 2y – 2 = 0
– x’ – 2y’ – 2 = 0

Transformasi selanjutnya adalah rotasi sebesar 90o yang berpusat di O(0, 0):

$\begin{pmatrix} x'' \\ y'' \end{pmatrix} = \begin{pmatrix} cos \; 90^{o} & -sin \; 90^{o} \\ sin \; 90^{o} & cos \; 90^{o} \end{pmatrix} \begin{pmatrix} x' \\ y' \end{pmatrix}$

$\begin{pmatrix} x'' \\ y'' \end{pmatrix} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} x' \\ y' \end{pmatrix}$

$\begin{pmatrix} x'' \\ y'' \end{pmatrix} = \begin{pmatrix} -y' \\ x' \end{pmatrix}$

Substitusi nilai x’ = y’’ dan y’ = – x’’ pada persamaan –x’ – 2y’ – 2 = 0, akan diperoleh

– x’ – 2y’ – 2 = 0
– y’’ – 2(–x’’) – 2 = 0
– y’’ + 2x’’ – 2 = 0
2x’’ – y’’ + 2 = 0

Jadi, hasil pencerminan garis x – 2y – 2 = 0 terhadap sumbu y dan kemudian diputar dengan R[ O(0,0), 90o ] adalah 2x – y + 2 = 0.

Jawaban: D

6. Dilatasi yang berpusat di titik (3, 1) dengan faktor skala 3, memetakan titik (5, b) ke titik (a, 10). Maka nilai a – b adalah ….
A. 15
B. 11
C. 5
D. 4
E. 2

Pembahasan:

Dilatasi dengan pusat (3, 1) dengan faktor skala 3 akan menghasilkan matriks transformasi berikut.

$\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} 3 & 0 \\ 0 & 3 \end{pmatrix} \begin{pmatrix} 5 - 3 \\ b- 1 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \end{pmatrix}$

$\begin{pmatrix} a \\ 10 \end{pmatrix} = \begin{pmatrix} 3 & 0 \\ 0 & 3 \end{pmatrix} \begin{pmatrix} 2 \\ b- 1 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \end{pmatrix}$

$\begin{pmatrix} a \\ 10 \end{pmatrix} = \begin{pmatrix} 6 \\ 3b - 3 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \end{pmatrix}$

$\begin{pmatrix} a \\ 10 \end{pmatrix} = \begin{pmatrix} 9 \\ 3b - 2 \end{pmatrix}$

Sehingga dapat diperoleh nilai a dan b:

a = 9
3b – 2 = 10
3b = 12
b = 12 : 3 = 4

Jadi, nilai a – b = 9 – 4 = 5

Jawaban: C

7. T1 adalah transformasi yang bersesuaian dengan matriks 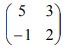soal transformasi geometri no 8 dan T2 adalah transformasi yang bersesuaian dengan matriks 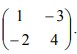Bayangan A (m,n) oleh transformasi T1 o T2 adalah (-9,7). Nilai m+n sama dengan…

A. 4

B. 5

C. 6

D. 7

E. 8

Jawaban : B

Pembahasan :

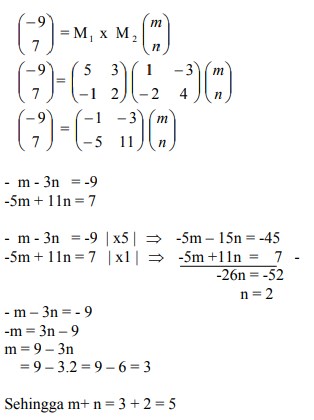
soal transformasi geometri dan jawaban no 8

8. Bayangan ∆ABC dengan A(2,1), B(6,1), C(5,3) karena refleksi terhadap sumbu y dilanjutkan rotasi (0,90°) adalah…

A. A” (-1,-2), B” (1,6) dan C” (-3,-5)

B. A” (-1,-2), B” (1,-6) dan C” (-3,-5)

C. A” (1,-2), B” (-1,6) dan C” (-3,5)

D. A” (-1,-2), B” (-1,-6) dan C” (-3,-5)

E. A” (-1,2), B” (-1,-6) dan C” (-3,-5)

Jawaban : D

Pembahasan :

soal transformasi geometri dan jawaban no 9

9. Persamaan peta kurva y = x² – 3x + 2 karena pencerminan terhadap sumbu x dilanjutkan dilatasai dengan pusat O dan factor skala 3 adalah…

A. 3y + x² – 9x + 18 = 0

B. 3y – x² + 9x – 18 = 0

C. 3y – x² + 9x + 18 = 0

D. 3y + x² + 9x + 18 = 0

E. y + x² + 9x – 18 = 0

Jawaban : A

Pembahasan :

pencerminan terhadap sumbu x:

P ( x , y ) → P ‘ ( x , – y )

Dilatasi terhadap titik pusat O(0,0) dengan factor skala 3 :

[O, k] : P(x,y) → P'(kx, ky)

[O,3k] : P(x,y) → P'(3x, 3y)

pencerminan terhadap sumbu x dilanjutkan dilatasai
dengan pusat O dan factor skala 3 :

P(x,y) → P ‘(x, -y) → P ”(3x, -3y)

soal transformasi geometri dan jawaban no 10

SOAL DAN PEMBAHASAN TRIGONOMETRI

Senin, 28 September 2020

TRANSFORMASI TRANSLASI, REFLEKSI, ROTASI, DILATASI, DENGAN MATRIKS

TRANSFORMASI TRANSLASI, REFLEKSI, ROTASI, DILATASI, DENGAN MATRIKS

Tidak ada komentar:

Posting Komentar

SIFAT-SIFAT LIMIT DAN CONTOH SOALNYA SERTA SOAL KONTEKSTUAL YANG BERHUBUNGAN DENGAN LIMIT

Total Tayangan Halaman