PEMBUKTIAN: LANGSUNG, TAK LANGSUNG, KONTRADIKSI, INDUKSI MATEMATIKA

PEMBUKTIAN: LANGSUNG, TAK LANGSUNG, 

KONTRADIKSI, INDUKSI MATEMATIKA

Assalamualaikum, ketemu lagi dengan saya Ryan Alfaridzi XI IPS 2, jadi saya kali ini, akan menjelaskan materi tentang Pembuktian dengan cara Langsung, Tak langsung,Kontradiksi, Induksi matematika

Apa itu Pembuktian? Nah didalam Matematika ada beberapa cara untuk melakukan pembuktian atau bisa disebut juga membuktikan. Diantaranya yaitu:

a. Pembuktian langsung

b. Tak langsung

c.  Kontradiksi

d.  Induksi

Nah berikut ini adalah penjelasannya

1. PEMBUKTIAN LANGSUNG

Bukti langsung adalah salah satu cara pembuktian sifat atau teorema matematika dengan penarikan kesimpulan dengan memanfaatkan silogisme, modus ponens dan modus tollens. Secara logika pembuktian q benar secara langsung atau ekuivalen dengan membuktikan bahwa pernyataan q benar dimana diketahui p benar

Metode pembuktian langsung adalah suatu proses pembuktian pembuktian menggunakan alur maju, mulai dari hipotesis dengan menggunakan implikasi logic sampai pada pernyataan kesimpulan.

Contoh: Buktikan bahwa : “jika n bilangan ganjil, maka n2 bilangan ganjil”.
Bukti:  
Diketahui bahwa n bilangan ganjil maka dapat dituliskanbahwa n = 2k+1 dengan k bilangan bulat
sehingga n² = (2k+1) 2 = 4k² + 4k + 1 = 2(2k²+2)+1
Bentuk 2(2k²+2k)+1 adalah bilangan ganjil
Jadi, n² adalah bilangan ganjil

2. PEMBUKTIAN TIDAK LANGSUNG

Pembuktian tidak langsung atau pembuktian dengan kemustahilan (reductio ad absurdum)yang dibahas ada 2 cara yaitu :

KONTRAPOSISI

Pembuktian tidak langsung atau kontraposisi digunakan untuk membuktikan pernyataan implikasi

Untuk membuktikan pernyataan implikasi kita cukup membuktikan kontraposisi dari implikasi pernyataan tersebut

Secara simbolik : p → q ≡ ~q → ~p  

Untuk membuktikan kebenaran p → q, maka kita cukup membuktikan

kebenaran ~q → ~p

contoh: buktikan bahwa “jika n2 bilangan ganjil, maka n bilangan ganjil”
Bukti:
Untuk membuktikan pernyataan tersebut kita akan membuktikan kebenaran kontraposisinya. Misalnya : p = n2 bilangan ganjil dan q = n bilangan ganjil
Apakah p → q benar ? Kita akan periksa apakah ~q → ~p benar ?  
Andaikan n bukan bilangan ganjil, maka n bilangan genap, sehingga n dinyatakan dengan sebagai n = 2k, k bilangan asli.  
Akibatnya n2 = (2k)2 = 4k2 = 2(2k2).
Artinya n2  bilangan genap.  
Jadi pengandaian bahwa n bukan bilangan ganjil adalah BENAR,  
sehingga kontraposisi ~q →~p juga BENAR.
Jadi implikasi p → q benar , ini berarti n2 bilanganganjil maka n adalah bilangan ganjil.

KONTRADIKSI

Pembuktian tidak langsung dengan kontradiksi dilakukan dengan mengandaikan konklusi yang salah dan menemukan suatu hal yang bertentangan dengan fakta, aksioma, atau teorema yang ada. Pengandaian konklusi salah tidak bisa diterima dan akibatnya konklusi yang ada benar berdasarkan premis yang ada

Contoh: Buktikan bahwa : “Untuk semua bilangan bulat n, jika n2 ganjil, maka n ganjil”.
Bukti: 
Andaikan bahwa q salah, atau ~q benar yaitu n bukan bilangan bulat ganjil, maka n bilangan bulat genap.
Dapat dimisalkan n = 2k dengan k bilangan bulat.  
Dengan demikian maka n2 = (2k)2 atau n2 = 4k2  
Ini menunjukkan bahwa  n2 = bilangan bulat genap (~p)
Terjadilah suatu kontradiksi : yang diketahui p benar, sedangdari langkah-langkah logis diturunkan ~p benar. Oleh karena itu kontradiksi tidak boleh terjadi, maka pengandaian harus diingkar yang berarti ~q salah atau q benar.

C. Induksi Matematika
adalah salah satu metode untuk membuktikan suatu pernyataan tertentu yang berlaku untuk bilangan asli 
Prinsip Induksi Matematika:
Misalkan P(n) adalah suatu pernyataan yang menyangkut bilangan asli n.  
Apabila P(1) benar, dan apabila P(k) benar maka P(k+1) juga benar, berakibat P(n) benar untuk semua n. 

Misalnya: Buktikan bahwa : “1 + 3 + 5 +  … + (2n-1) = n2, untuk semua bilangan

                 asli n”.

Bukti: Misalkan P(n) adalah 1 + 3 + 5 + 7 + … + (2n-1) = n2

P(1) benar, sebab 1 = 1

Bila P(k) benar, yaitu apabila ; 1 + 3 + 5 + 7 + … + (2k-1) = k2, maka

1 + 3 + 5 + 7 + … + 2k-1 + 2k+1= (1 + 3 + 5 + 7 + … + 2k- 1 + 2k+1.

= k2 + 2k + 1

= (k + 1)2

Sehingga P(k+1) benar

Demikian pembahasaan Matematika saya Assalamualaikum wr.wb

penjelasan dan contoh soal LOGIKA Matematika

Pengertian Logika Matematika

Logika matematika ialah suatu cabang logika dan matematika yang mengandung sebuah kajian matematis logika dan aplikasi kajian ini pada bidang-bidang lain di luar matematika.

Logika matematika ini berhubungan erat dengan bidang ilmu komputer dan logika filosofis. Tema utama dalam logika matematika ini antara lain yaitu sebagai kekuatan ekspresif dari logika dan kekuatan deduktif dari sistem pembuktianformal.

Logika matematika ini sering dibagi ke dalam cabang-cabang dari teori himpunan, teori rekursi, teori model, teori pembuktian dan teori matematika konstruktif.

Bidang-bidang ini masing-masing mempunyai hasil dasar logika yang serupa.

Hukum logika

1. Hukum komutatif, yaitu:

• p∧q ≡ q∧p
• p∨q ≡ q∨p

2. Hukum asosiatif, yaitu:

• (p  ∧  q) ∧ r sama dengan p ∧ (q  ∧  r)
• (p  ∨  q) ∨ r sama dengan p ∨ (q  ∨  r)

3. Hukum distributif, yaitu:

• Apabila p∧(q∨r) maka sama dengan (p∧q)∨(p∧r)
• Apabila p∨(q∧r) maka sama dengan (p∨q)∧(p∨r)

4. Hukum identitas, yaitu:

• p ∧ B ≡  p
• p ∨ S ≡  p

5. Hukum ikatan, yaitu:

• p ∧ S ≡  S
• p ∨ B ≡  B

6. Hukum negasi, yaitu:

• p ∧ ~p ≡  S
• p ∨ ~p ≡  B

7. Hukum negasi ganda, yaitu:

• ~(~p) ≡  p

8. Hukum idempotent, yaitu:

• p ∧ p ≡  p
• p ∨ p ≡  p

9. Hukum De Morgan, yaitu:

• ~(p ∧ q) ≡ ~p  ∨  ~q
• ~(p ∨ q) ≡ ~p  ∧  ~q

10. Hukum penyerapan, yaitu:

• p ∧ (p ∨ q) ≡  p
• p ∨ (p ∧ q) ≡  p

11. Negasi B dan S, yaitu:

• ~B ≡  S
• ~S ≡  B

12. p → q ≡ ~p  ∨  q

13. p ↔ q ≡ (~p  ∨   q) ∧ (p ∨ ~q)

Didalam logika matematika, terdapat cara untuk mementukan nilai dari suatu pernyataan, baik bernilai benar ataupun bernilai salah.

Pernyataan itu sendiri juga terbagi menjadi 2 jenis, yaitu:

1. Pernyataan Tertutup (Kalimat Tertutup)

Pernyataan tertutup atau kalimat tertutup yaitu suatu pernyataan yang sudah memiliki nilai benar atau salah.

Contohnya:
“5 ialah bilangan genap”, kalimat tersebut bernilai salah karena yang benar seharusnya ialah “5 adalah bilangan ganjil”.

2. Pernyataan Terbuka (Kalimat Terbuka)

Pernyataan terbuka atau kalimat terbuka ialah suatu pernyataan yang belum dapat ditentukan nilai kebenarannya karna adanya suatu perubah atau variabel.

Contoh logika matematika:

Ketika 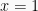, maka  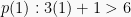bernilai salah, dan
Ketika 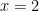, maka  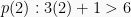bernilai benar

Ingkaran atau Negasi dari suatu Pernyataan

Ingkaran atau negasi ialah kebalikan nilai dari suatu pernyataan itu sendiri, dimana ketika suatu pernyataan bernilai benar, maka negasinya bernilai salah dan saat suatu pernyataan bernilai salah, maka negasinya bernilai benar. Ingkaran atau negasi dari pernyataan 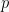 dilambangkan dengan simbol: .

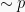Pernyataan Kuantor

Pernyataan kuantor ialah bentuk logika matematika yang berupa pernyataan yang memiliki kuantitas. Didalam pernyataan kuantor, pada umumnya terdapat kata semua, seluruh, setiap, beberapa, ada, dan sebagian.

Kata-kata yang senilai dengan seluruh, semua, setiap termasuk dalam kuantor universal dan kata-kata yang senilai dengan sebagian, beberapa, ada, adalah termasuk kedalam kuantor eksistensial.

Kuantor universal dan kuantor eksistensial saling beringkaran.

Contoh:

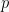 : semua orang ialah sarjana (Kuantor universal)

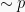 : sebagian orang ialah tidak sarjana

Pernyataan Majemuk, Bentuk Ekuivalen dan Ingkarannya

Pernyataan Majemuk dalam ilmu matematika ialah beberapa pernyataan yang dapat dibentuk menjadi satu pernyataan dengan menggunakan kata penghubung logika seperti dan, atau, maka dan jika dan hanya jika.

Dalam logika matematika, kata hubung tersebut masing-masing memiliki lambang dan istilahnya sendiri, yaitu:

Tabel Kebenaran Konjungsi

Dari tabel diatas dapat kita simpulkan bahwa sifat dari konjungsi ialah bernilai benar jika kedua pernyataan penyusun dari peryataan majemuk keduanya bernilai benar.

Tabel Kebenaran Disjungsi

Berdasarkan tabel diatas maka dapat kita ambil simpulkan bahwa sifat dari disjungsi ialah bernilai salah jika kedua pernyataan penyusun dari peryataan majemuk keduanya bernilai salah.

Tabel Kebenaran Implikasi

Pada sifat implikasi ini, 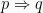, suatu p disebut sebagai hipotesa dan q sebagai konklusi. Maka pada implikasi ini akan menghasilkan nilai salah ketika konklusi salah dan hipotesa benar.

Tabel Kebenaran Biimplikasi

Pada sifat biimplikasi ini, suatu penyataan majemuk akan bernilai benar apabila kedua pernyataan penyusunnya bernilai sama, keduanya benar atau keduanya salah.

Tautologi dan Kontradiksi

Tautologi ialah pernyataan majemuk yang selalu benar untuk semua kemungkinan yang ada dan kontradiksi ialah kebalikannya, yaitu pernyataan majemuk yang bernilai salah untuk semua kemungkinan yang ada.

Bentuk Ekuivalen Pernyataan Majemuk

Pernyataan majemuk yang memiliki nilai sama untuk seluruh kemungkinannya disebut ekuivalen.

Notasi ekuivalen dalam logika matematika ialah ““.

Bentuk-bentuk pernyataan yang saling ekuivalen yaitu:

Ingkaran Pernyataan Majemuk

Ingkaran Konjungsi= 

Ingkaran Disjungsi= 

Ingkaran Implikasi=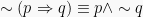 

Ingkaran Biimplikasi=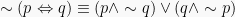 

Konvers, Invers dan Kontraposisi

Konvers, invers dan kontraposisi adalah merupakan bentuk lain dari implikasi, dimana pengertiannya masing-masing yaitu:

Konvers dari 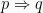 ialah 

Invers dari 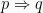 ialah 

Kontraposisi dari 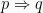 ialah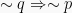 

Penarikan Kesimpulan Logika Matematika

Penarikan kesimpulan ialah konklusi dari beberapa pernyataan majemuk (premis) yang saling keterkaitan.

Dalam penarikan kesimpulan tersebut terdiri atas beberapa cara, yaitu:

Contoh Soal Logika Matematika

Soal 1:
Premis 1 : Apabila Andi rajin belajar, maka Andi juara kelas
Premis 2 : Andi  rajin  belajar
Kesimpulannya dari kedua premis diatas yaitu ….

Jawab:
Premis 1               :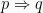  
Premis 2               :  p
Kesimpulan          :  q (modus ponens)
Maka, kesimpulannya ialah Andi juara kelas.

Soal 2:
Premis 1 : Apabila hari hujan, maka sekolah libur
Premis 2   : sekolah tidak libur
Kesimpulan dari kedua premis diatas yaitu ….

Jawab:
Premis 1               :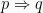  
Premis 2               :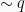  
Kesimpulan          : (modus tollens)
Maka, kesimpulannya ialah hari tidak hujan

Demikianlah pembahasan kita mengenai Logika Matematika, Baik dari pengertiannya sampai ke contoh soalnya. Semoga bermanfaat ya …