Assalamualaikum Wr. Wb.
Perkenalkan nama saya Ryan Alfaridzi, absen 33, dari kelas X IPS 2.
Pada kesempatan kali ini saya akan menyampaikan bahwa pentingnya berdiam diri di dalam rumah pada saat ini. Dikarenakan virus Corona sudah menyebar luas. Hal ini dilakukan untuk meminimalisir penyebaran virus Corona tersebut.
Pemerintah melarang untuk keluar rumah atau sekarang yg lebih sering kita dengar "stay at home". Kegiatan ini membuat saya bosan di rumah saja.
Untuk melawan rasa bosan tersebut saya mempelajari beberapa pelajaran, salah satunya Matematika.
Materi yg paling saya suka dari Matematika kelas X adalah Trigonometri.
Apa sih pengertian Trigonometri tersebut?
Trigonometri adalah sebuah cabang matematika yang mempelajari hubungan yang meliputi panjang dan sudut segitiga.
Yg paling saya suka dari Trigonometri ini adalah Konsep Sinus, Cosinus dan Luas Segitiga.
Pada materi ini akan membahas mengenai bagaimana aturan sinus dan cosinus bisa diaplikasikan ke dalam segitiga.
Terdapat aturan sinus bisa digunakan jika 2 sudut dan 1 sisinya diketahui atau 2 sisi dan 1 sudut segitiga diketahui, sedangkan aturan cosinus bisa diaplikasikan bila panjang sisi-sisi segitiga dan kosinus salah satu sudut dalam segitiga diketahui.
Selain itu, kamupun bisa mencari luas sebuah segitiga jika sinus salah satu sudut diketahui. Selain itu adanya aturan sinus, aturan cosinus, dan luas segitiga ini penting untuk kamu kuasai.
Contoh 1 :
Contoh 2 :
Demikian cerita pembelajaran saya tentang Sinus, Cosinus dan Luas Segitiga. Semoga dapat bermanfaat.
Sekian dari saya Wassalamu'alaikum Wr. Wb.
Tugas 5 Mei 2020 (contoh soal dan pembahasan trigonometri)
1. Sebuah kipas angin berputar dengan kecepatan 36 putaran per menit. Nyatakan kecepatan putaran kipas angin tersebut ke dalam satuan radian per detik!
Penyelesaian:
36 putaran/menit = 36 x 2π/60 putaran/detik
36 putaran/menit = 1,2π putaran/detik
36 putaran/menit = 36 x 2π/60 putaran/detik
36 putaran/menit = 1,2π putaran/detik
Jadi 36 putaran per menit sama dengan 1,2π putaran per detik.
2. Sebuah segitiga siku-siku.
Diketahui nilai dari sin β = 2/3. Tentukan nilai dari :
a) cos β
b) tan β
Pembahasan
sin β = 2/3 artinya perbandingan panjang sisi depan dengan sisi miringnya adalah 2 : 3
Gunakan phytagoras untuk menghitung panjang sisi yang ketiga (sisi samping):
Sehingga nilai cos β dan tan β berturut-turut adalah
3. Segitiga KLM memiliki koordinat K(−5,−2),L(3,−2), dan M(−5,4). Nilai cos L dan tan M berturut-turut adalah?
Pembahasan :
Pertama sketsakan segitiga KLM pada sistem koordinat Kartesius seperti berikut.
Tampak bahwa segitiga KLM merupakan segitiga siku-siku (di L).
Dari gambar di atas, diketahui bahwa
KL=3−(−5)=8;KM=4−(−2)=6
Dengan menggunakan Teorema Pythagoras, diperoleh
LM=√KL2+KM2=√82+62=√64+36=√100=10
Untuk itu,
cosL=KLLM=810=45tanM=KLKM=86=43
Jadi, nilai cos L dan tan M berturut-turut adalah 45 dan 43.
4. Besar sudut yang sesuai dengan gambar di bawah adalah?
Pembahasan :
Sudut yang terbentuk searah dengan jarum jam, sehingga tandanya negatif, yakni −30∘.
Karena satu putaran sama dengan 360∘, maka −30∘ sama dengan (360−30)∘=330∘
Jadi, besar sudutnya adalah 330∘
Karena satu putaran sama dengan 360∘, maka −30∘ sama dengan (360−30)∘=330∘
Jadi, besar sudutnya adalah 330∘
5. Jika (f o g) (x) = x + 4, dan g(x) = x – 2. Maka carilah invers dari fungsi f(x).
Pembahasan :
(f o g) (x) = x + 4
f(g(x)) = x + 4
f(x – 2) = x + 4
Misal u = x – 2, maka x = u + 2, sehingga
f(x – 2) = x + 4
f(u) = u + 2 + 4
f(u) = u + 6
f(x) = x + 6
y = x + 6
x = y – 6
f-1(x) = x – 6
Jadi, invers dari fungsi f(x) adalah f-1(x) = x – 6.
6. Nyatakan tiap perbandingan trigonometri berikut di dalam sudut 37° !
tan 153°
sin 243°
cos 333°
Pembahasan :
Sudut 153° adapada kuadran II, hingga tan 153° memiliki nilai negatif.
tan 153° = tan (180° − 27°)
= -tan 27°
Sudut 243° ada pada kuadran III, sehingga sinus memiliki nilai negatif.
sin 243° = sin (270° − 27°)
= -cos 27°
Sudut 333° ada pada kuadran IV, hingga cosinus memiliki nilai positif.
cos 333° = cos (360° − 27°)
=cos 27°
7. Tanpa memakai kalkulator, tentukan nilai dari sin100∘−cos190∘cos350∘−sin260∘.
Pembahasan :
sin 100° = sin (90° + 10°)
= cos 10°
= cos 10°
cos 190° = cos (180° + 10°)
= -cos 10°
= -cos 10°
cos 350° = cos (360° − 10°)
= cos 10°
= cos 10°
sin 260° = sin (270° − 10°)
= -cos 10°
= -cos 10°
Jadi :
sin100∘−cos190∘cos350∘−sin260∘=cos10∘−(−cos10∘)cos10∘−(−cos10∘)=2cos10∘2cos10∘=1
sin100∘−cos190∘cos350∘−sin260∘=cos10∘−(−cos10∘)cos10∘−(−cos10∘)=2cos10∘2cos10∘=1
8. Tentukanlah nilai x yang memenuhi persamaan cos 2x = 1/2 dalam interval 0° < x ≤ 360.
Pembahasan :
cos 2x = 1/2
cos 2x = cos 60
cos 2x = 1/2
cos 2x = cos 60
Maka :
2x = 60 + k.360
x = 30 + k.180
Untuk k = 0
maka x = 30 + (0)180 = 30
2x = 60 + k.360
x = 30 + k.180
Untuk k = 0
maka x = 30 + (0)180 = 30
Untuk k = 1
maka x = 30 + (1)180 = 210
dan 2x = –60 + k.360
x = –30 + k.180
Untuk k = 1
maka x = –30 + (1)180 = 150
maka x = 30 + (1)180 = 210
dan 2x = –60 + k.360
x = –30 + k.180
Untuk k = 1
maka x = –30 + (1)180 = 150
Untuk k = 2
maka x = –30 + (2)180 = 330
Jadi H adalah { 30, 150 , 210 , 330 }
maka x = –30 + (2)180 = 330
Jadi H adalah { 30, 150 , 210 , 330 }
9. untuk koordinat kutub ke koordinat kartesius
Jika diketahui koordinat kutub (6√3, 60°), maka koordinat kartesiusnya adalah?
Pembahasan :
koordinat kutub ⇒ koordinat kartesius
(r , α) ⇒ ( x , y )
r = 6√3 ; α = 60°
(Karena α sudut di kuadran I, maka x positif f dan y positif)
x = r cos α
⇒ 6√3 x cos 60°
⇒ 6√3 x 1/2
⇒ 3√3
y = r sin α
⇒ 6√3 x sin 60°
⇒ 6√3 x 1/2 √3
⇒ 3 x 3
⇒ 9
sehingga koordinat kartesiusnya ialah ( 3√3 , 9)
10. Bagus berdiri dengan jarak 80 m dari sebuah menara memandang puncak menara dengan sudut elevasi 30o. Jika jarak mata Bagus dengan tanah adalah 150 cm, tinggi menara tersebut adalah?
Pembahasan :
Perhatikan ilustrasi berikut.
Jadi, tinggi menara adalah
![\[ = 80 \cdot tan30^{o} + 1,5 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-2ac20231972885bd7729d40421ecfbc9_l3.png "Rendered by QuickLaTeX.com")
![\[ = 80 \cdot \frac{1}{3} \sqrt{3} + 1,5 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-54eddfa9ab7bfe9b89a5ad274fc2a9c0_l3.png "Rendered by QuickLaTeX.com")
![\[ = \left( \frac{80}{3} \sqrt{3} + 1,5 \right) \textrm{m} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-e858d56be02d212da5a3d0289b6afa39_l3.png "Rendered by QuickLaTeX.com")
10. Sebuah kapal berlayar dari pelabuhan A ke pelabuhan B dengan kecepatan 40 km/jam selama 2 jam dengan arah 030°, kemudian melanjutkan perjalanan dari pelabuhan B menuju pelabuhan C dengan kecepatan 60 km/jam selama 2,5 jam dengan arah 150°. Buatlah sketsa perjalanan kapal dan tentukan jarak antara pelabuhan A dan C!
Pembahasan:
Jarak = kecepatan x waktu
Jarak pelabuhan A ke B adalah 40 x 2 = 80 km
Jarak pelabuhan B ke C adalah 60 x 2,5 = 150 km
Perhatikan gambar terlampir.
Besar sudut ABC adalah 30° + 30° = 60°
Gunakan aturan cosinus untuk mencari AC
AC² = AB² + BC² - [2 x AB x BC x cos ∠ABC]
AC² = 80² + 150² - [2 x 80 x 150 x cos 60°]
AC² = 28.900 - [2 x 80 x 150 x ¹/₂]
AC² = 28.900 - 12.000
AC = √ 16.900
Diperoleh jarak antara pelabuhan A dan C sejauh 130 km
11. Diketahui suatu taman di tengah kota berbentuk segitiga sembarang. Jika sudut apit sebesar 60o dan dua sisi yang mengapitnya masing-masing panjangnya 18 meter dan 16 meter, maka luas taman tersebut adalah ….
Pembahasan:
Untuk menentukan luas segitiga sembarang yang diketahui panjang dua sisi dan sudut antara kedua sisi tersebut dapat memanfaatkan fungsi sinus.
![\[ L = \frac{1}{2} \times 18 \times 16 \times sin \; 60^{o} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-ac01cd707d0e045a1e210520eb819cf8_l3.png "Rendered by QuickLaTeX.com")
![\[ L = \frac{1}{2} \times 18 \times 16 \times \frac{1}{2} \sqrt{3} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-63d01e5d865aa1d109a909c153fab861_l3.png "Rendered by QuickLaTeX.com")
![\[ L = 72 \sqrt{3} \; \textrm{m}^{2} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-89d6405345ee8d8716bde9247e1a03c0_l3.png "Rendered by QuickLaTeX.com")
12. Andi sedang mengukur mainan segitiganya yang tiap sudutnya dikodekan dengan A, B, dan C, kemudian diketahui segitiga tersebut memiliki sudut A = 30º, sisi a = 6cm dan sisi b = 8cm. Hitung besar sudut B.
Pembahasan :
Akan dicari besar sudut B
sin B = (b sin A)/a
sin B = 8/6 sin 30̊
sin B = 2/3
B = arc sin B
B = arc sin (2/3)
B = 41,8̊
Jadi, besar sudut B adalah 41,8̊ atau 180̊ – 41,8̊ = 138,2̊
13. Pada segitiga ABC diketahui panjang sisi a yaitu 10 cm dan panjang sisi c yaitu 12 cm. Jika besar sudut yang diapit oleh a dan c yaitu 46o, maka tentukan panjang sisi b.
Pembahasan :
Dik : a = 10 cm, ∠B = 46o, c = 12 cm
Dit : b = ... ?
Berdasarkan aturan cosinus :
⇒ b2 = a2 + c2 − 2ac cos B
⇒ b2 = 102 + 122 − 2(10)(12) cos 46o
⇒ b2 = 100 + 144 − 240 (0.6946)
⇒ b2 = 244 − 166,7
⇒ b2 = 77,3
⇒ b = 8,8 cm
Jadi, panjang sisi b yaitu 8,8 cm.
sin B = (b sin A)/a
sin B = 8/6 sin 30̊
sin B = 2/3
B = arc sin B
B = arc sin (2/3)
B = 41,8̊
Jadi, besar sudut B adalah 41,8̊ atau 180̊ – 41,8̊ = 138,2̊
13. Pada segitiga ABC diketahui panjang sisi a yaitu 10 cm dan panjang sisi c yaitu 12 cm. Jika besar sudut yang diapit oleh a dan c yaitu 46o, maka tentukan panjang sisi b.
Pembahasan :
Dik : a = 10 cm, ∠B = 46o, c = 12 cm
Dit : b = ... ?
Berdasarkan aturan cosinus :
⇒ b2 = a2 + c2 − 2ac cos B
⇒ b2 = 102 + 122 − 2(10)(12) cos 46o
⇒ b2 = 100 + 144 − 240 (0.6946)
⇒ b2 = 244 − 166,7
⇒ b2 = 77,3
⇒ b = 8,8 cm
Jadi, panjang sisi b yaitu 8,8 cm.
14. Fungsi yang sesuai dengan grafik berikut adalah?
Pembahasan :
Pembahasan
Beranjak dari grafik sinus: karena kurva bergeser (ke kiri) sejauh π2, maka bentuk umum grafik fungsinya adalah f(x)= y = a sin k(x−c).
Untuk grafik ini, nilai c yang menentukan pergeseran kurva adalah −π2 (tandanya negatif, karena grafik bergeser ke kiri).
Dimulai dari titik x =−π2 yang nilai fungsinya 0, grafik fungsi kembali bernilai 0 dan berulang kembali di titik x =3π2, sehingga periode grafik fungsinya adalah 3π2–(−π2)=2π.
Dengan demikian,
k = 2π Periode = 2π
2π =1
Nilai a ditentukan oleh nilai maksimum dan nilai minimum fungsi, yakni
a=N. Maksimum−N. Minimum2=2−(−2)2=2
Jadi, rumus grafik fungsinya adalah f(x)=2sin1(x+π2)=2sin(x+π2)
Untuk grafik ini, nilai c yang menentukan pergeseran kurva adalah −π2 (tandanya negatif, karena grafik bergeser ke kiri).
Dimulai dari titik x =−π2 yang nilai fungsinya 0, grafik fungsi kembali bernilai 0 dan berulang kembali di titik x =3π2, sehingga periode grafik fungsinya adalah 3π2–(−π2)=2π.
Dengan demikian,
k = 2π Periode = 2π
2π =1
Nilai a ditentukan oleh nilai maksimum dan nilai minimum fungsi, yakni
a=N. Maksimum−N. Minimum2=2−(−2)2=2
Jadi, rumus grafik fungsinya adalah f(x)=2sin1(x+π2)=2sin(x+π2)
15. Grafik f(x)=2cosx memotong sumbu-X di titik berkoordinat ?
Pembahasan :
Apabila grafik memotong sumbu-X, maka nilai f(x)=y=0. Dengan demikian,
f(x)=2cosx⇒0=2cosx⇔cosx=0
Nilai x yang membuat cosx bernilai 0 adalah 90∘.
Jadi, titik potong grafiknya berkoordinat (90∘,0
f(x)=2cosx⇒0=2cosx⇔cosx=0
Nilai x yang membuat cosx bernilai 0 adalah 90∘.
Jadi, titik potong grafiknya berkoordinat (90∘,0
16. Tentukan nilai maksimum dan minimum fungsi
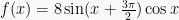
Pembahasan :
Gunakan :
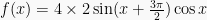
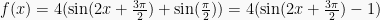
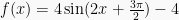
Sehingga :
Pembahasan :
Pembahasan :
Gunakan :
Sehingga :
- Untuk sin
, maka
- Untuk sin
, maka
17. Andi berdiri tegak pada jarak 10√3 m dari kaki sebuah pohon besar yang tumbuh gerak lurus. Jika tinggi Andi 1,6 m dan melihat ke puncak pohon dengan sudut elevasi 60°. Tentukan tinggi pohon tersebut?
Pembahasan :
tan 60⁰ = x / 10√3
√3 = x / 10√3
x = √3 . 10√3
x = 30
Jadi tinggi pohon adalah
= x + tinggi Andi
= 30 m + 1,6 m
= 31,6 m
18. Dalam suatu lingkaran berjari-jari 10 cm, dibuat segi – 8 beraturan. Panjang sisi segi – 8 tersebut adalah?
Untuk mencari panjang sisi segi delapan, kita perlu mengetahui besar sudut puncak segitiga pada segi delapan, yaitu:
![\[ = \frac{360^{0}}{8} = 45^{o} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-235ba5831c09a8e01703754ed0057e82_l3.png "Rendered by QuickLaTeX.com")
Selanjutnya, untuk menentukan panjang sisi segi delapan dapat digunakan persamaan pada aturan cosinus.
![\[ AB^{2} = OA^{2} + OB^{2} - 2 \cdot OA \cdot OB \cos 45^{o} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-926dce3d6d3349bd84f6dd8b87f49103_l3.png "Rendered by QuickLaTeX.com")
![\[ AB^{2} = 10^{2} + 10^{2} - 2 \cdot 10 \cdot 10 \cdot \cos 45^{0} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-2388d81e3c42875c9a160d64432af5f3_l3.png "Rendered by QuickLaTeX.com")
![\[ AB^{2} = 100 + 100 - 2 \cdot 100 \cdot \frac{1}{2} \sqrt{2} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-85b7afb892a238ea99014ea21e548032_l3.png "Rendered by QuickLaTeX.com")
![\[ AB^{2} = 200 - 100 \sqrt{2} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-cf952255421ffc5b7d0bbc2769e5426a_l3.png "Rendered by QuickLaTeX.com")
![\[ AB = \sqrt{200 - 100 \sqrt{2}} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-e29ee1d6d0d0e7802505ce054b5f19fd_l3.png "Rendered by QuickLaTeX.com")
![\[ AB = \sqrt{ 100 \left( 2 - \sqrt{2}\right)} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-67e3a67bff3fc9a6bb2ee0b733cb89c1_l3.png "Rendered by QuickLaTeX.com")
19. Diketahui cot (x + 36°) = tan 2x. Jika 2x adalah sudut lancip, tentukan nilai x !
Jawab :
cot (x + 36°) = tan 2x
Karena 2x sudut lancip, pastilah 2x terletak dikuadran I. Dengan menggunakan relasi sudut kuadran I, maka :
tan 2x = cot (90° − 2x)
Sehingga
cot (x + 36°) = cot (90° − 2x)
x + 36 = 90° − 2x
3x = 54
x = 18
20.Nyatakan setiap perbandingan trigonometri berikut dalam sudut 37° !
tan 143°
sin 233°
cos 323°
Jawab :
Sudut 143° terletak pada kuadran II, sehingga tan 143° bernilai negatif.
tan 143° = tan (180° − 37°)
tan 143° = -tan 37°
Sudut 233° terletak pada kuadran III, sehingga sinus bernilai negatif.
sin 233° = sin (270° − 37°)
tan 233° = -cos 37°
Soalnya mantap...bisa di copy paste kah?
BalasHapus